Stein’s method for rough paths

The Donsker theorem says that a random walk, when conveniently rescaled, converges to a Brownian motion. A finer result of Friz and Victoir, that the Lévy area of the random walk goes also to the Lévy area of the Brownian motion. The question is to know the speed of this convergence. We show that this holds as $n^{-(1/2-\eta)}$ for a RW of $n$ steps in the space of $\eta$-Holderian functions.

Table 1: The Lévy area in blue and its approximation in red. On the right, the corresponding sample-path of the two dimensional Brownian motion.

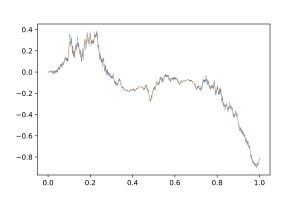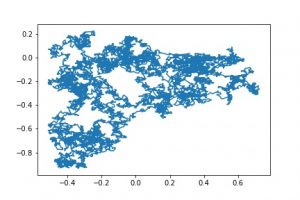The full version of the paper is available on HAL

Actually, this work is a continuation of our previous article on Stein’s method in infinite dimensional spaces.
Very classically, we use the Stein’s method. The challenges are

• to define the convenient functional spaces,
• these spaces are infinite dimensional so that the trace terms are not simple to compute,
• to deal with the fact that the Levy area as a process is not Gaussian, hence is not eligible to a characterization by a Stein equation.

The first challenge is addressed by considering fractional Sobolev spaces for Heisenberg valued functions.

The second difficulty is overwhelmed by computing the distance between the random walk and the affine interpolation of the Brownian motion with the same time step. The distance between this interpolation and the true sample-path of the Lévy area has already been evaluated in frizil_gauss

As to the Stein equation, we must remark that the randomness in the Lévy area is the same as in the two underlying Brownian motions:
$$ \int_0^t B^1(s) dB^2(s) – \int_0^t B^2(s) dB^1(s) \in \sigma\Bigl\{B^1(s),B^2(s),\ s\le t\Bigr\}$$
so that the target measure is in fact a standard Gaussian distribution on a finite dimensional space.

Bibliography

• [frizil_gauss] Peter Friz & Nicolas Victoir, Multidimensional Stochastic Processes as Rough Paths, Cambridge University Press (2010).